ABSTRACT
A case study is used to introduce a two-step thermal demand calculation for buildings in order to take thermal bridges into consideration. In the first step the outer envelope of a typical apartment is 3-dimensionally modelled and a 3D thermal-coupling coefficient is calculated. In the second step the thermal demands of the whole building is calculated using three variations of the outer envelope design. Each variation is calculated in 1D and 3D. The difference between the results of 1D and 3D calculations is used to show the influence of thermal bridges upon the overall heat loss of building.
INTRODUCTION
A large number of pre-fabricated apartment buildings, built during the communist era of the former Czechoslovakia, were inherited by both successor states. All of these buildings fail to meet today's thermal performance standards,thus making them a target for energy efficiency improvement efforts. It is important to have a method to determine whether or not proposed modifications will actually result in improved energy performance. In this case, the use of computer simulation appears to be the best approach. This is because most of the prefabricated buildings are made up of the same panel systems.Therefore, it is possible to economically develop a very detailed and precise computer model of the typical panel system. This model can then be re-used to test various improvement measures under different climatic conditions. The precision of the computer model described above depends on the calculated precision of the thermal-coupling coefficient (conductance) of the construction details. Thermal-coupling coefficient is a proportion factor that influences the heat flow between neighbouring spaces. In order to take into account thermal bridging it makes sense to calculate thermal-coupling coefficient three-dimensionally. One dimensional calculation can only serve as a rough estimation; it does not correspond to reality at all. In addition, construction details in 3D computer models can be used for examination of critical points such as room edges, attic details, etc. These are particularly important from the point of view of the building practitioner. In this study the computer software WAEBRU V5.0 [4]was used to calculate the 3D thermal-coupling coefficients of construction details. It was able to provide all of the information relevant to describing the thermal characteristics including: maximum and minimum surface temperature (with respective dewpoints for specific sets of boundry conditions), a matrix of temperature weighting factors (g-values) and a conductance matrix. The overall heating demand for the entire apartment building was calculated with the help of the computer software WAEBED [3]. This program allows the examination of heat loss through transmission of the building envelope using both one and three-dimensional calculated values of thermal coupling-coefficients. In order to elaborate this computer model further, a case study using the pre-fabricated panel system T06B was undertaken. This panel system is one of the most common types of pre-fabricated systems in use in the former Czechoslovakia today. We created a model of an apartment envelope (different for typical and attic apartment) by turning of which by 90° one floor of such an apartment house arise (Fig. 1 and 2). The difference between this model and other computer models is that it consists of a set of three dimensionally modelled construction details and three-dimensionally calculated thermal-coupling coefficients. This information can be used to examine the thermal demands under different climatic conditions for any apartment building built from the same panel system (even though the form of the building may vary, the details usually remain the same). Of course, after slight modifications are made to the model it can be used to test a variety of proposed design improvements.
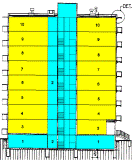Cross-section
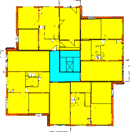Typical floor plan
Fig. 1. Division of the entire building into temperature zones.
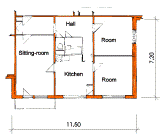
Fig. 2. Typical apartment plan by turning of which by 90 degrees one floor of an apartment house arises
COMPUTER MODEL
According to H. Werner [5]: "the notion "thermal demands" can be used when an amount of heat, determinable thanks to certain given marginal conditions is being "calculated". Such calculations are used to optimize the thermal quality of the building envelope in the planning phase rather than to make a prognosis about the real consumption to be expected. The notion "consumption" means the real in practice existing amount of consumed heating energy." According to Slovak standards, the normal basis for determining thermal demands is through an one-dimensional calculation of the thermal-coupling coefficient [L=U.A]. This approach only partly considers thermal bridges and in such a way that only external measures are taken into consideration. To explain why this may be a problem, it is helpful to discuss in more detail the notion of thermal conductance (thermal coupling coefficient). "Only panel-like building components with strictly surface parallel layers (a product consisting of U-value and surface) can be accurately represented using an one-dimensional [surface-related] thermal-coupling coefficient" [2]. However, based on practical experience, the cross-section of a panel changes in all three axis directions in the case of a thermal bridge caused by materials and construction. "Therefore, it can only be described with the help of a three-dimensionally calculated thermal-coupling coefficient. Where the cross-sections of a panel change in two axis directions it is possible to first calculate the length-related thermal-coupling coefficient as L2D [W.m-1.K-1 ] where
L = Σ L2D.l [W/K] ..... (1)
and l stands for the length of the building component" [2]. "The use of a computer is inevitable for calculating 2D and 3D thermal-coupling coefficients. At this point, one may question whether or not it would be easier to three-dimensionally determine the entire thermal-coupling coefficient for the entire envelope at one time. This would put an enormous demand on the memory capacity of the computer. Considering the current capacity of PC-s such an operation is not possible. Therefore it is necessary to separate the heat transmitting building envelope before calculation into 1D areas on one side and 2D and 3D areas containing the predicted thermal bridges on the other side (see the sketch).
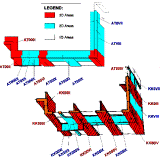
Sketch. Division of the outer apartment envelope (different for typical and attic apartment) into 3D, 2D and 1D areas
The 1D areas can be calculated according to standard and 2D and 3D areas with the help of a numerical process producing 2D and 3D thermal-coupling coefficients. Total basic value LTOT for our considered apartment comes then to:
LTOT = Σ L3D + Σ L2D.l + Σ A.U [W/K] ..... (2)
The thermal-coupling coefficient determined in this way takes into account the influence of the thermal bridges relatively accurately. When compared with the standard method (one-dimensional) LTOT we can define the supplementary figure LHB. This corresponds with the sum of the χ and ψ values, which can be derived from the 2D or 3D thermal-coupling coefficients. These coefficients can conceivably be used again as a building-system-characteristic quantity for the calculation of other buildings. The total thermal-coupling coefficient LTOT with the use of χ and ψ values (indirect process) makes:
LTOT = Σ A.U + Σ ψ + Σ χ = Σ A.U + δLHB [W/K] ..... (3)
The thermal demands of one building calculated on the basis of the
examination of 3D thermal-coupling coefficient allows us to avoid the problems
resulting from "overly optimistic" predictions from 1D examinations.
The ability to catch potential problems early (and accurately) is helpful
both for modification to existing structures as well for the design of
new buildings"[8]. For the purposes of this study, the examination
of the 3D thermal-coupling coefficient was done using WAEBRU V5.0 [4].
This is a software package used for the calculation of temperature distributions
and heat flows in building structures; particularly those with thermal
bridges. "Key features of WAEBRU are:
- Calculation of base solutions (method of finite differences) - WAEBRU
allows the precision of numerical solutions to be influenced and controlled
by the user (definition of calculation parameters)
- Specification of boundary conditions (reference air temperatures in
the spaces under consideration) and heat source power assumptions in a
separate evaluation branch of WAEBRU. A comparison of evaluation results
under varying conditions is thus accomplished promptly, since it is unnecessary
to repeat the calculation of base solutions for different sets of conditions
(principle of superposition)" [4].
Examples of two- and three-dimensionally modelled construction details
are shown in Figure 3. a. and b. (CorelDraw illustrations with heat flow
lines determined by WAEBRU V5.0).
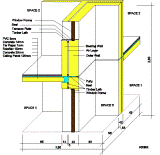
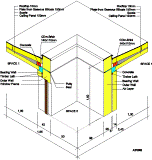
Fig. 3. a. Examples of three dimensionally modelled construction details (CorelDraw Illustrations)
The thermal demands of the entire apartment building were calculated
using the computer program WAEBED [3] which handles non-steady state conditions.
In this case climatic data [6] of an Austrian village, Wolfsthal (very
close to Bratislava ) was used - Slovak or Czech climatic data is not yet
available in the program.
The entire building was divided into 10 zones according to the Figure
1. Two of the zones are considered unheated (basement and staircase) and
the rest (apartments) were presumed to be at Ti=
20 degrees Celsius. Ideal heat control was also assumed.
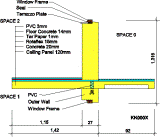
KK000X - Geometry and heat flow lines
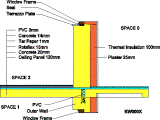
KW000X - Geometry and heat flow lines
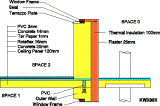
KWX00X - Geometry and heat flow lines
Fig. 3. b. Examples of two dimensionally modelled construction details for existing state, model I and model II (CorelDraw illustrations, heat flow lines are determined by WAEBRU V5.0)
OUTER ENVELOPE ANALYSIS OF THE APARTMENT MODEL [8]
The thermal demands for 3 variations of the outer envelope design were examined: (1) the existing state, (2) Model I and, (3) Model II. Each instance was examined in 1D and 3D. Model I represents an improvement to the physical construction of original envelope that includes the addition of 10 cm thermal insulation and 2,5 cm of external plaster. The thermal insulation layer is interrupted by a balcony panel. In Model II, the balcony panel was eliminated. This alternative solution is relevant where a new balcony is constructed to be self-supporting or when it is omitted altogether. Table 1 shows the calculated thermal demands for all three variations for one apartment calculated one-dimensionally and three-dimensionally. In the last column the errors produced by one-dimensional calculation can be found in percentage of the correct thermal demands. With the existing construction, the difference between the three-dimensional and the one-dimensional investigation is 4,60%, but after installing the above mentioned thermal insulation layer it becomes 16,74%. Despite that bridging effect, the thermal demands have been decreased to almost one half. After elimining one part of the thermal bridging (i.e. after demolition of the balcony panel) the contribution of the thermal bridges declined to 10,20%. This result clearly shows that the 1D investigation can lead to an underestimation of the heat losses. In this study we did not investigate the minimal surface temperatures of building panels containing thermal bridges. Yet from the practical experience we know that every thermal bridge represents a source of potential construction damage. As a matter of interest ecological consequences of retrofitting in form of carbon dioxide emissions are shown. The 1D investigation can be used to predetermine the thermal demand, but for an advanced planning phase a 3D investigation is inevitable. You can find evidence for this in Table 2. According to this table the sum of the 3D-calculated thermal-coupling coefficients of building panels for the existing apartment (without windows) shows a difference of 5% when compared with the sum of 1D determined thermal-coupling coefficients. In Model I (i. e. after installing thermal insulation) this difference increases to 28%. The "elimination" of the balcony panel in Model II leads to a decline to 17%. Table 3 and Figure 6 show the overall thermal demands of the whole apartment house for all three configurations including the difference between 1D and 3D calculation.
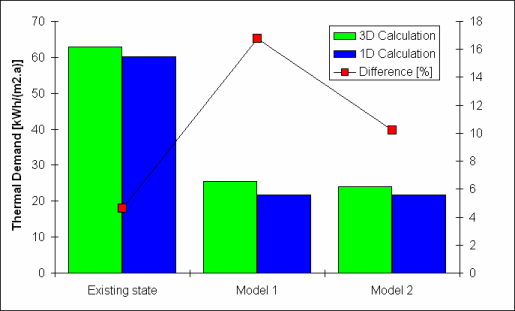
Fig. 4. Thermal demand of one typical apartment calculated for 3 different variations compared with the growth of thermal bridges
| Variation | Thermal Demand [kWh/(m2.a)] 3D Calculation |
Thermal Demand [kWh/(m2.a)] 1D Calculation |
Difference [%] | CO2-Emission (gas heating)[9] [kg/(m2.a)] |
| Existing State | 62,87 | 60,11 | 4,60 | 11,95 |
| Model I | 25,43 | 21,78 | 16,74 | 4,83 |
| Model II | 24,00 | 21,78 | 10,20 | 4,56 |
Table 1. Thermal demand of one typical apartment calculated for 3 different variations compared with the growth of thermal bridges; CO2-Emission values based upon the 3D calculation of heat energy demand
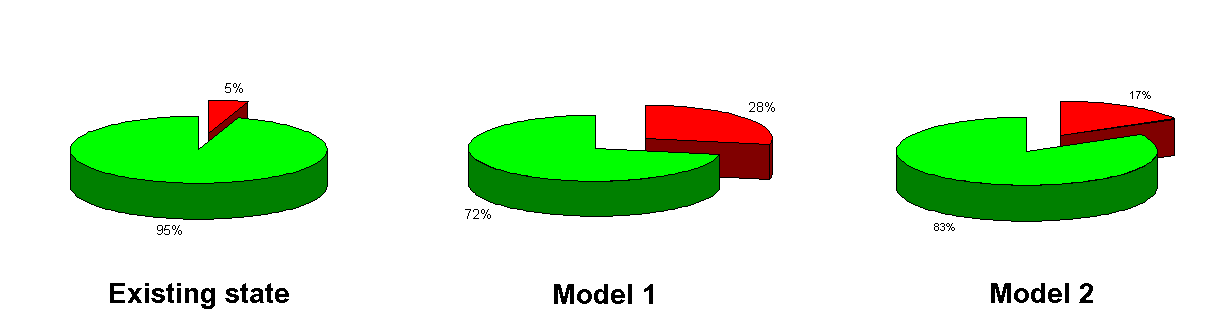
Fig. 5. Contribution of heat bridges in % to the overall thermal-coupling coefficient of the envelope of one apartment
| Variation | Thermal-coupling coefficient [W/K] 3D Calculation |
Thermal-coupling coefficient [W/K] 1D Calculation |
Difference LHB [%] |
| Existing State | 55,46 | 52,84 | 5 |
| Model I | 17,54 | 13,67 | 28 |
| Model II | 16,00 | 13,67 | 17 |
Table 2. Contribution of thermal bridges in % to the overall thermal-coupling coefficient of the envelope of one apartment
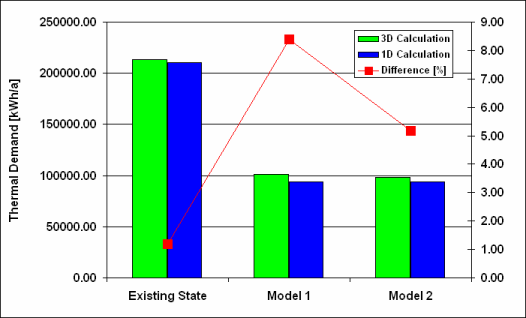
Fig. 6. Overall thermal demand of the whole apartment house calculated for 3 different variations compared with the growth of thermal bridges
| Variation | Overall thermal demand [kWh/a] 3D Calculation |
Overall thermal demand [kWh/a] 1D Calculation |
Difference between 3D and 1D Calculation [%] |
| Existing State | 212984,1 | 210461,9 | 1,20 |
| Model I | 101463,7 | 93564,8 | 8,40 |
| Model II | 98413,2 | 93564,8 | 5,18 |
Table 3. Overall thermal demand of the whole apartment house calculated for 3 different variations compared with the growth of thermal bridges
CONCLUSIONS [8]
As previously stated, in Eastern and Central Europe there is a huge number of pre-fabricated residential buildings. The majority of these buildings are situated geographically in areas where the rooms have to be heated for almost half of the year. The increasing price of energy is forcing owners to improve their buildings technologically. Although it is not as bad as doing nothing at all, retrofitting and adding insulation to the building's envelope introduces a completely new problem - thermal bridges. Ignoring this problem can cause great disappointment. One of the aims of this study is to underscore this point. In order to avoid thermal bridges a computer simulation of the envelope is recommended at the beginning stages of design planning. In pre-fabricated panel buildings there are a lot of similar buildings with the same panel system type. Therefore, it is reasonable to develop a very precise computer model of the given panel system and then use it in the evaluation of various improvement measures under a variety of climatic conditions. It is also recommended that the standard (one-dimensional) calculation of the thermal-coupling coefficient, which does not take 2D and 3D heat flows into consideration sufficiently, should be amended as soon as possible.
ACKNOWLEDGEMENTS
At this time I would like to express my warmest thanks to Prof.E.Panzhauser and Prof.K.Krec from TU Vienna, who kindly placed both Austrian Computerpackages WAEBRU and WAEBED at my disposal and Mrs. S. Mallory-Hill from TU Eindhoven for English correction.
REFERENCES
- EN ISO 10211-1: Thermal Bridges in Building Construction - Heat Flows and Surface Temperatures, Part 1 - General Calculation Methods, 1995
- W.Heindl, K. Krec, E. Panzhauser, A. Sigmund: Wärmebrücken. Springer-Verlag, Wien, 1987
- Programmpaket WAEBED. Version 1.0. Programmpaket zur Berechnung des Heizwärmebedarfes von Gebäuden. Benutzerhandbuch. Institut für Hochbau für Architekten der TU Wien, Abteilung für bauphysikalische und Humanökologische Grundlagen des Hochbaues, Demonstrativlaboratorium für Hochbau, 1995
- WAEBRU Version 5.0. Programmpaket zur Berechnung von Temperaturverteilungen und Wärmeströmen in Bauteilen. Benutzerhandbuch. Copyright Univ. Prof. Dr. E. Panzhauser, 1993
- H.Werner: Der Europäische Wärmepaß. CEN-Berechnungsverfahren für den Heizwärmebedarf von Gebäuden. Bauphysik 15, Heft 2, Ernst und Sohn Verlag für Architektur und technische Wissenschaften, Berlin, 1993
- W.Heindl, K.Krec, A.Sigmund: Klimadatenkatalog. Bundesministerium für Bauten und Technik - Staatlicher Hochbau, Kommissionsverlag: Österreichischer Ingenieur- und Architektenverein, Wien, 1984
- W.Heindl, H.Fuchs, J.Lang, K.Jost: Katalog für empfohlene Wärmeschutzrechenwerte von Baustoffen und Baukonstruktionen. Bundesministerium für Bauten und Technik - Staatlicher Hochbau, Kommissionsverlag: Österreichischer Ingenieur- und Architektenverein, Wien, 1979
- E.Panzhauser, R.Rabenseifer: Die bauökologische Belastung der umgebenden Außenwelt durch sanierte und nichtsanierte Plattenwohnhäuser anhand eines Beispiels in Bratislava. Proceedings of International Symposium of CIB W67 - Energy and Mass Flow in the Life Cycle of Buildings, Technische Universität Wien, Aug. 4-10, 1996
- Generaldirektion der Wiener Stadtwerke: Neue Wege für Wiens Energie, Energiekonzept der Stadt Wien. 2.Fortschreibung, Bohmann Druck und Verlag, 1991
For more information: Roman
Rabenseifer
Back to the top